CUDA MST

Learning by doing.

(source code can be found here)

After getting trained by various CUDA / parallel computing courses and doing many toy assignments / projects with well-prepared code context, I have determined to dive a little bit deeper to practise my CUDA programming skills.

Graph algorithms interests me most and MST looks to be very much simple to get started with. Therefore I decided to play with parallelising MST algorithm.

After doing a little bit (re)search, I noticed two interesting papers:

• Chapter 7 Fast Minimum Spanning Tree Computation in the book GPU Computing Gems
• Fast and Memory-Efficient Minimum Spanning Tree on the GPU

The first one implements the data-parallel Boruvka’s algorithm, while the second one introduced some serialism of Kruskal’s thereby chopping the big problem into smaller ones and accerating even more.

Basically, 2 algorithms are mostly focused on:

Kruskal’s algorithm: (quoting from Fast and Memory-Efficient Minimum Spanning Tree on the GPU)

F = set()
C = [0, 1, 2, ... , n-1]
G = Sort(G)
for i in range(m):
  (s, w, t) = G.Edges[i]
  if C[s] != C[t]:
    F += set((s, w, t))
    C = ConnectComponents(F, C)

Boruvka’s algorithm: (quoting from Fast and Memory-Efficient Minimum Spanning Tree on the GPU)

F = set()
C = [0, 1, 2, ... , n-1]
G_ = BuildDirectedAdjacencyList(G)
while EdgesRemaining(G_):
  F += FindMinEdges(G_)   // parallelism!!
  C  = ConnectComponents(F, C)
  G_ = ContractGraph(G_)

Referring to the first paper, the CUDA MST can be implemented as follows:

(the original slides can be found here)

Unlike the paper, I decided to use adjacency-list-like edges rather than compacted adjacency list, because it is a little bit easier to implement for me…

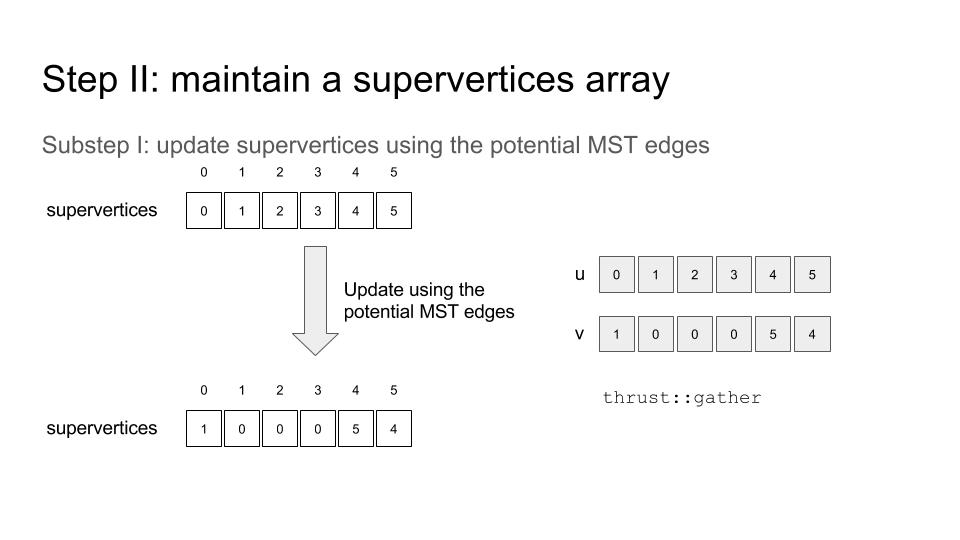
And another thing to remember is: Don’t try to sort a huge struct by key directly. Rather, one may want to firstly sort indices by key and then scatter / gather. Huge performance can be squeezed out from here!! See this…

thrust::reduce_by_key is really helpful, though there are several things to notice – I recorded some of them on 11th, April

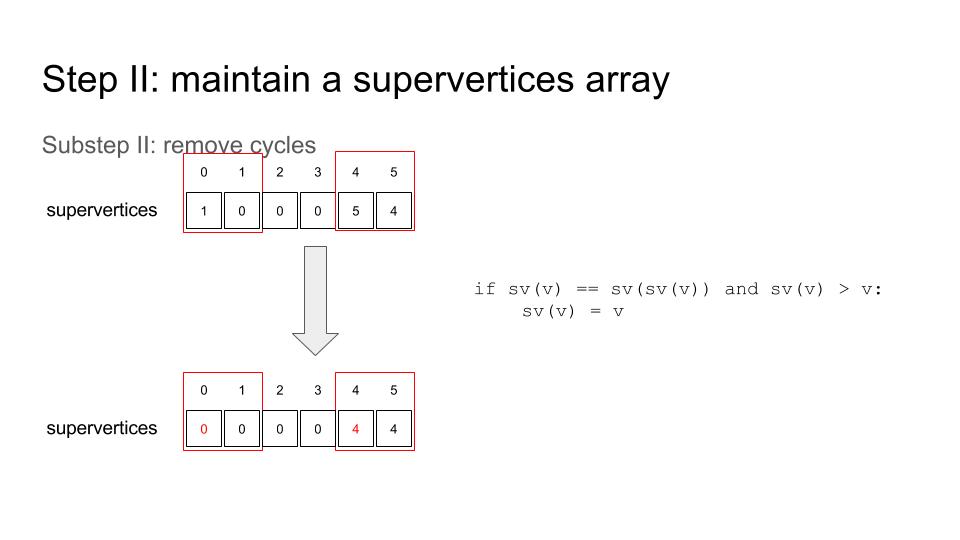
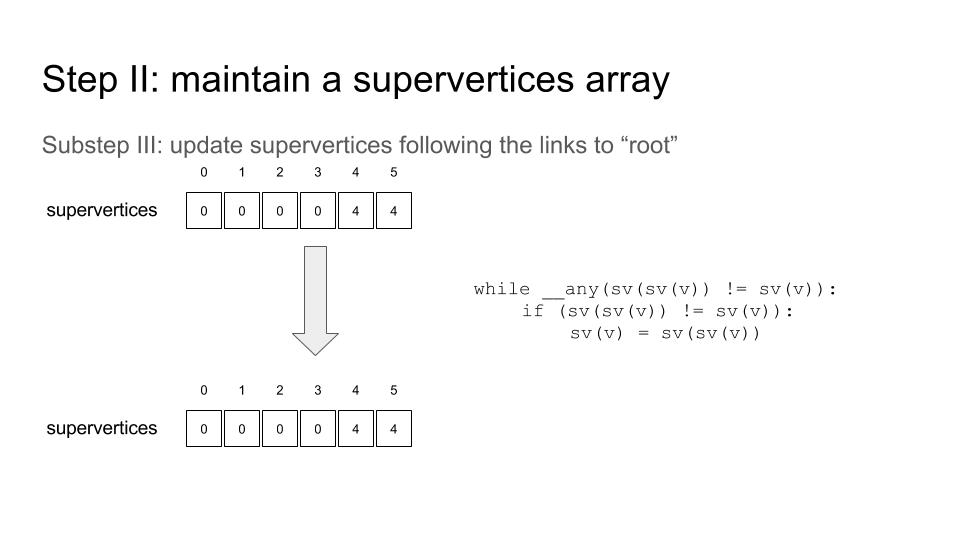
There are pretty many helpful CUDA intrisic functions – __any for warp voting is one of them… And __ballot, and __popc, etc. .

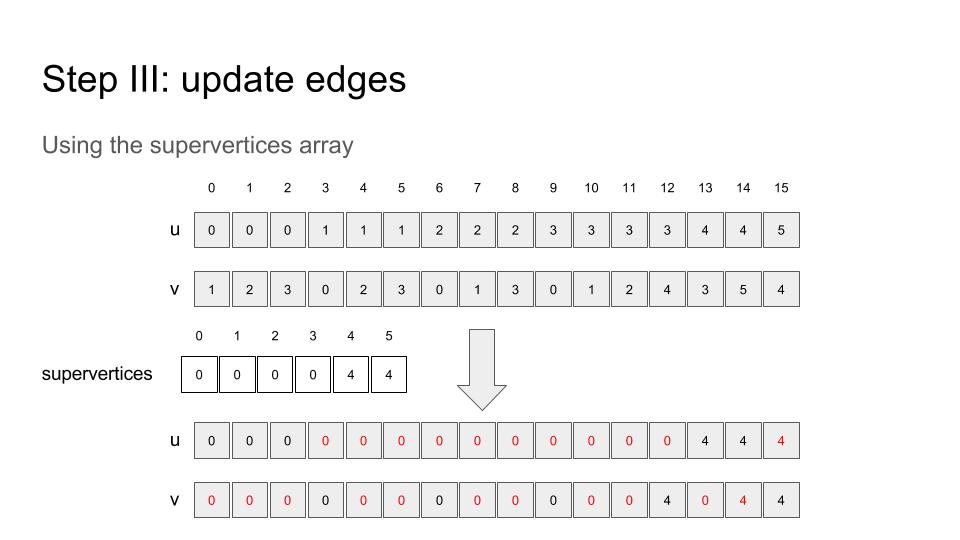
Up to now, one can go back to step I, and do it again.

This step, IMO, can be executed in parallel (using cuda streams) as step II is in progress. I haven’t tried it yet…

So, that’s so much for the first paper. Unfortunately, I didn’t see much benefit compared to a well-optimised serial 2-phase Kruskal’s with weight-and-path-compression union-find.

Result: (GTX750ti & E1231v2 machine)

• I cannot go beyond 2 million vertices with 10 million edges for random graph with my 2GB GPU memory.
• On-par for random and power-law graph, better with sparse grid graph.

gpuMST result

1 : randLocalGraph_WE_5_2000000 :  -r 1 -o /tmp/ofile765486_563367 : '0.759'
1 : rMatGraph_WE_5_2000000 :  -r 1 -o /tmp/ofile138860_218538 : '0.655'
1 : 2Dgrid_WE_2000000 :  -r 1 -o /tmp/ofile8903_852545 : '0.159'
gpuMST : 0 : weighted time, min=0.524 median=0.524 mean=0.524

serialMST result

1 : randLocalGraph_WE_5_2000000 :  -r 1 -o /tmp/ofile399034_715347 : '0.65'
1 : rMatGraph_WE_5_2000000 :  -r 1 -o /tmp/ofile477678_439826 : '0.697'
1 : 2Dgrid_WE_2000000 :  -r 1 -o /tmp/ofile983504_141272 : '0.395'
serialMST : 0 : weighted time, min=0.58 median=0.58 mean=0.58

As is pointed out in the second paper: At each iteration of Boruvka’s algorithm every remaining edge is considered and the lightest edge for each supervertex is selected.

This is costly, in terms of both computation and memory – with smaller problem set

• the sorting can be done faster
• we only need to store a local 2m edge list, which is a small fraction of the original graph – this saves memory
• we can filter out many edges on each step computing subgraphs’ MST, further reduce problem size

And actually the only modifications needed are:

• add a split_graph function and call it on start – the sorting there is a once-for-all call, shouldn’t be worried :relieved:
• add a contract_and_build_subgraph function and call it before doing Boruvka’s – all one need to do is to update edge vertices by supervertices.
• make the supervertices array inside Boruvka’s global – this is actually a simple way to implement IMO – I don’t want to call merge_vertices again :no_mouth:

And… Voila!

The graph size that tool can handle is more than doubled, and the performance is improved by more than 3x. Though now the algorithm presents with similar degradation when handling power-law graphs as degraded in pure serial Kruskal’s algorithm.

gpuMSTdpk result

1 : randLocalGraph_WE_5_5000000 :  -r 1 -o /tmp/ofile609269_741536 : '0.604'
1 : rMatGraph_WE_5_5000000 :  -r 1 -o /tmp/ofile631862_452509 : '0.886'
1 : 2Dgrid_WE_5000000 :  -r 1 -o /tmp/ofile972092_45516 : '0.363'
gpuMSTdpk : 0 : weighted time, min=0.617 median=0.617 mean=0.617

serialMST result

1 : randLocalGraph_WE_5_5000000 :  -r 1 -o /tmp/ofile514914_278972 : '1.99'
1 : rMatGraph_WE_5_5000000 :  -r 1 -o /tmp/ofile295582_919992 : '2.54'
1 : 2Dgrid_WE_5000000 :  -r 1 -o /tmp/ofile576909_787203 : '1.19'
serialMST : 0 : weighted time, min=1.906 median=1.906 mean=1.906

I should have plotted some graphs or curves but I don’t have the time.

The major intent to play with CUDA MST is to practise my CUDA programming skill / data parallel primitive usage experience after all…

Anyway, it has been a nice experience, and I wish I will have more chances later…