Course link This is merely a supplimental course notes…

---

Week 1

Guiding Questions

• What does a computer have to do in order to understand a natural language sentence?
  • part-of-speech tagging, syntatic analysis, semantic analysis, pragmatic analysis
• What is ambiguity?
  • word-level ambiguity (e.g. POS, meaning)
  • syntatic ambiguity (e.g. (adj.)modification, PP attachment (…with a telescope))
  • anaphora ambiguity (e.g. himself refering to whom?)
  • presupposition (e.g. “He quit smoking” implies “He smoked”)
• Why is natural language processing (NLP) difficult for computers?
  • people omit a lot of common sense knowledge
  • people keep a lot of ambiguities
• What is bag-of-words representation? Why is this word-based representation more robust than representations derived from syntactic and semantic analysis of text?
• What is a paradigmatic relation?
• What is a syntagmatic relation?
• What is the general idea for discovering paradigmatic relations from text?
• What is the general idea for discovering syntagmatic relations from text?
• Why do we want to do Term Frequency Transformation?
• How does BM25 transformation work?
• Why do we want to do IDF (Inverse Document Frequency) weighting?
• What is entropy? For what kind of random variables does the entropy function reach its minimum and maximum, respectively?
• What is conditional entropy?
• What is the relation between conditional entropy H(X|Y) and entropy H(X)? Which is larger?
• How can conditional entropy be used for discovering syntagmatic relations?
• What is mutual information I(X;Y)? How is it related to entropy H(X) and conditional entropy H(X|Y)?
• What’s the minimum value of I(X;Y)? Is it symmetric?
• For what kind of X and Y, does mutual information I(X;Y) reach its minimum? For a given X, for what Y does I(X;Y) reach its maximum?
• Why is mutual information sometimes more useful for discovering syntagmatic relations than conditional entropy?

Overview

• Text mining $\approx$ Text analytics
  • mining focuses on the process – algorithms
  • analytics focuses on the results
  • generally, they are the same
• high-quality information and actionable knowledge
  • high-quality information: more concise information about the topic, easier to digest
  • actionable knowledge: for decision / action to take

</img>

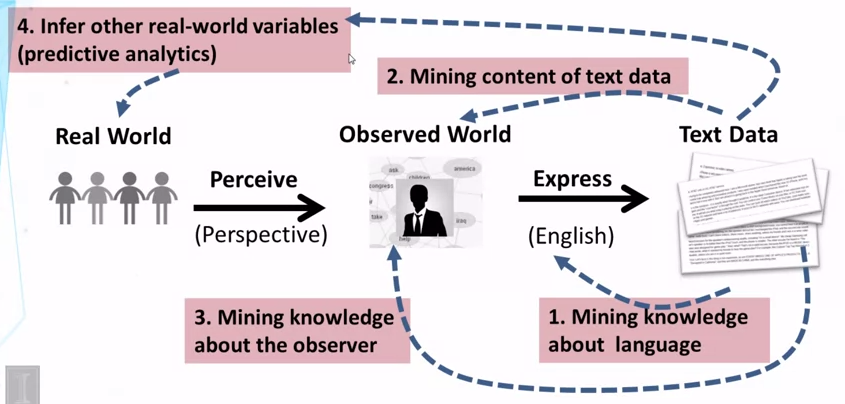
• landscape of text mining and text analytics
  • text mining: revert the process of generating text data
  • inferring (4) can use the intermediate data / results from (2) and (3)
    • processing of the text data to generate features that helps prediction, is very important
  • can also use non-text data to
    • help prediction
    • associate with text data (e.g. timeframe, geolocation, other meta data)

Natural Language Content Analysis

• shallow analysis
  • to be covered in this course
  • applicable to any texts
  • can be done in large scale
  • statistical approach
  • deeper analysis: may require more human power to anotate data

Text Representation

• text representation
  • string of characters: any language, but cannot analyse semantics
  • sequence of words: powerful for English, but difficult for some languages (e.g. Chinese)
  • • POS tags: (+) means this is an additional way for text representation
  • • syntactic structures
  • • entities and relations:
      • application: knowledge graph (Google)
      • less robust, yet useful
  • • logic predicates
  • • speech acts: intent of the sentence
  • as we go down, more human effort is required, less accurate; but gives user direct knowledge – deep representation of knowledge
  • note: Human play an important role. So one need to optimise human-computer collaboration.

Word Association Mining and Analysis

• paradigmatic relation: substituting words keeps the sentence valid for understanding
  • applies to units in similar locations in data sequence
• syntagmatic relation: semantically related, in general cannot replace each other
  • applies to co-occurrence in data sequence
• why:
  • acronym: abbreviation expansion
• applications:
  • for text retrieval:
    • query expansion
    • query suggestion
• intuitions:
  • compare similarity of context (left, right, general)
• general ideas:
  • paradigmatic: words with high context similarity
  • syntagmatic: words with high cooccurrence but relatively low individual occurrences
  • joint disconvery: paradigmatic related words tend to have syntagmatic relation with same words

Paradigmatics Relation Discovery

• “pseudo document”
  • bag of words
  • ‘Left1(“cat”)’: word before “cat”
  • Right1: word after
  • Window8: words around
• expected overlap of workds in context (EOWC)
  • $d1 = (x_1, …, x_N)$, $x_i = c(w_i, d1) / |d1|$
  • a probablity distribution of words in document $d1$
  • dot product as the similarity
• problems of EOWC
  • favours frequent terms over distinct terms
    • e.g. d1 and d2 has one overlapping term with 0.5 probablity, $sim = 0.5 * 0.5 = 0.25$
    • e.g. d1 and d2 has 500 overlapping terms with 0.01 probablity for each, $sim = 0.01 * 0.01 * 500 = 0.05$
    • solution: sublinear transformation of term frequency (TF)
    • bend (sublinearise) the $c(w, d)$ curve
  • treats every word equally
    • solution: reward matching a rare word: IDF term weighting (inverse document frequency)
    • “collection”: all the collected documents / contexts
• adapting BM25 for paragmatic relation discovery
  • $x_i = \frac{BM25(w_i, d1)}{\sum_{j=1}^{N}BM25(w_j, d1)}$
  • normalisation of $x_i$, to make sure the sum is still 1
  • $BM25(w_i, d1) = \frac{(k + 1)c(w_i, d1)}{c(w_i, d1) + k(1 - b + b * |d1|/avdl)}$
  • $1 - b + b * \frac{|d1|}{avdl}$: document length penalisation
  • $sim(d1, d2) = \sum_{i = 1}^{N} IDF(w_i) x_i y_i$
• adapting BM25 for syntagmatic relation discovery
  • same: $x_i = \frac{BM25(w_i, d1)}{\sum_{j=1}^{N}BM25(w_j, d1)}$
  • IDF-weighted d1: $d1 = (x_i * IDF(w_i), …, x_N * IDF(w_N))$
  • highly weighted terms (w’s) are likely syntagmatically related to each other

Syntagmatic Relation Discovery: Entropy

• syntagmatic relation: correlated occurrences

• word prediction: intuition
  • “the” is easy to predict: it probably will occur
  • “unicorn” is easy to predict as well: it probably will NOT occur
  • “meat” is relatively hard to predict
  • how random is the word?
    • entropy: quantitatively measure the randomness
• entropy
  • $H(X_w) = \sum_{v\in \{0, 1\} } -p(X_w = v) \log_2 p(X_w = v)$
  • here: only binary random variable
  • high: meaning more random
  • e.g. $p(x=1)=1$ shows a constant, which is not random, its $H$ is 0
  • e.g. $p(x=1)=0.5$ shows a “fair coin”, which is random, its $H$ is 1

Syntagmatic Relation Discovery: Conditional Entropy

• entropy when condition
  • the condition changes the “prediction” / “randomness”
  • the “change” shows the syntagmatic relation, I think
  • just change $p(x=v)$ into $p(x=v | y=u)$
  • $H(X|Y) = \sum_{u\in\{0, 1\}} p(X=u) H(X|Y=u)$
  • $H(X|Y) \leq H(X)$
  • knowing more, the uncertainty / randomness can only be reduced
  • minimum being 0, (I think) when, e.g., two words only occur in pairs, or the condition is the word itself
    • $H(X_{meat} | X_{meat}) = 0$
• conditional entropy to capture syntagmatic relation
  • $H(X_{meat} | X_{meat}) = 0$
  • $H(X_{meat} | X_{the}) > H(X_{meat} | X_{eats})$
  • how to mine the strongest K syntagmatic relations from a collection?
    • one can sort $H(X_{w1} | X_{w2})$ and pick the smallest
    • but that only yields the related words of $w1$ – asymmetric
    • if one want to mine K, repeatedly doing that will be costly
    • since $H(X_{w2} | X_{w1})$ and $H(X_{w3} | X_{w1})$ are not comparable
      • they have different upperbounds
    • mutal information!!

Syntagmatic Relation Discovery: Mutal Information

• $I(X; Y) = H(X) - H(X|Y) = H(Y) - H(Y|X)$
  • non-negative: $I(X; Y) \geq 0$
  • symmetric: $I(X; Y) = I(Y; X)$
  • $I(X; Y) = 0$ $\iff$ $X$ and $Y$ are independent
• rewriting MI using KL-divergence
  • $I(X;Y) = \sum_{u\in \{0, 1\}}\sum_{v\in \{0, 1\}} p(X=u, Y=v) \log_2 \frac{p(X=u, Y=v)}{p(X=u) p(Y=v)}$
  • easy for implementation: only need to count:
    • $p(X=1)$
    • $p(Y=1)$
    • $p(X=1, Y=1)$
    • all other terms in the formula above can then be derived

---

Week 2

Topic Mining and Analysis: Motivation and Task Definition

• discover topics
  • how to define $\theta_k$ ?
• determine which documents cover which topics

Term as Topic

• easy, but many problems
  • lack of expressive power
    • let topic be multiple words
  • incompleteness in vocalublary coverage, e.g. related words
    • add weights on words
  • word ambiguity
    • split ambiguious word

Probabilistic Topic Models

• topic = word distribution
  • multiple words
  • weights as probablities
  • ambiguious words are split into multiple topics
• generative model for text mining
  • design a model with parameters $\Lambda = (\{\theta_1, …, \theta_k\}, \{\pi_{11}, …, \pi_{1k}\}, \{\pi_{N1}, …, \pi_{Nk}\})$
    • $k$ topics
    • $N$ documents
    • number: $(N * k + N * k)$, here $(N = |V|)$
  • maximise $p(data | model, \Lambda)$
    • $\Lambda^* = argmax_{\Lambda} p(data | model, \Lambda)$

Overview of Statistical Language Models

• general models that covers probabilistic top models as special cases

• two problems:
  • given a model, how likely will one observe certain kind of data points
    • sampling process
  • given some observed data, to figure out some parameters of a model
    • estimating process
    • is the estimation in the slides the best? How to define “best”?
      • the estimation in the slides is the best: maximum likelihood
• maximum likelihood and bayesian estimation
  • watch the video…
  • this document may be helpful

Mining One Topic

• use Lagrange function multiplier approach
  • $\hat{\theta} = argmax_\theta \sum_{i=1}^M c(w_i, d) \log\theta_i$
  • subject to constraint: $\sum_{i=1}^M \theta = 1$
  • solution: $\hat{\theta} = \frac {c(w_i, d)}{|d|}$
  • will use numerical approaches later…
• what does the topic look like?
  • top: common words (e.g. the, a, etc.)
    • how to get rid of them? next lecture…
  • middle: topic-related words
  • bottom: topic-irrelevant (less related) words

Mixture of Unigram Language Models

• use another distribution to generate only those common words
  • $p(w) = p(\theta_d)p(w|\theta_d) + p(\theta_B)p(w|\theta_B)$
  • or even more daring (more models mixed):
    • $p(w) = \sum p(\theta_i)p(w|\theta_i)$

Mixture Model Estimation

• assume the background model is fixed
• collaboration and competition of $\theta_d$ and $\theta_B$
  • $p(w1|\theta_B) > p(w2|\theta_B) \Rightarrow p(w1|\theta_d) < p(w2|\theta_d)$
    • balance out
  • high frequency words get higher $p(w|\theta_d)$
• summary
  • high probabilities to high-frequent words: collaboratively maxmise likelihood
    • when “the” occurrence increases, its impact on the likelihood function increases as well
      • so increasing its (“the”’s) probability helps to increase the likelihood
  • different component tend to bet high probablities on different words
    • same word in different component has very different probabilities?
    • i.e. $p(w1|\theta_B) > p(w2|\theta_B) \Rightarrow p(w1|\theta_d) < p(w2|\theta_d)$
  • component probabilities are used to regulate the collaboration and competition
    • higher $p(\theta_B)$ suppresses (regulates) the marginal increase of $p(“the”|\theta_d)$ / parameters of common words
    • thus encourages the topic-word parameters to increase

Expectation-Maximisation Algorithm

• for mixture model estimation
• infer which component / distribution a single word comes from
  • from $\theta_d$ (z=0):
    • $p(z=0|w) = \frac{p(\theta_d)p(w|\theta_d)} {p(\theta_d)p(w|\theta_d) + p(\theta_B)p(w|\theta_B)}$
    • normalised
    • “expectation” step
• maximisation step
  • if we know exactly which distribute a single word comes from
    • $p(w|\theta_d) = \frac{c(w, d)} {\sum_{w’\in V} c(w’, d)}$
  • now we combine the inference
    • $p(w|\theta_d) = \frac{c(w, d)p(z=0|w)} {\sum_{w’\in V} c(w’, d)p(z=0|w)}$
• iterative algorithm
  • e-step: determine $p^{(n)}(z=0|w)$
  • m-step: determine $p^{(n+1)}(w|\theta_d)$
  • stop when likelihood doesnt change
• EM computation in action
  • target: $p(w|\theta_d)$
  • by products: $p(z=0|w)$
    • helps to evaluate how the document covers background words
• hill climbing
  • possible to get stuck at local optima (mutliple runs are needed)

Probabilistic Latent Semantic Analysis (PLSA)

• basic topic mining
• likelihood function:
  • $p(w) = \lambda_Bp(w|\theta_B) + (1-\lambda_B)\sum_{i=1}^k p(\theta_i)p(w|\theta_i)$
    • $\lambda_B$: known
    • $p(w|\theta_B)$: known
    • $p(\theta_i) = \pi_{d, i}$: to-be-determined
    • $p(w|\theta_i)$: to-be-determined
  • for document: $\prod_{w\in V} p(w)$, i.e.
    • $\log p(d) = \sum_{w\in V} c(w, d) \log(p_d(w))$
  • for collection:
    • $\log p(C|\Lambda) = \sum_{d\in C} \sum_{w\in V} \log p(d)$
  • parameter to be determined:
    • $\Lambda = (\{\pi_{d, j}\}, \{\theta_j\}), j=1, …, k$
• EM algorithm for PLSA
  • $\pi_{d, j}$ is tied to each documents!!
    • each document covers topics in a different way
    • therefore $z_{d, w}$, the hidden variable for augmenting words are tied to words in each document
  • M-step (my understanding):
    • $f(w, d, j) = c(w, d) (1 - p(z_{d, w} = B)) p(z_{d, w} = j)$
    • $\pi_{d, j}^{(n+1)} = \frac{\sum_{w\in V} f(w, d, j)} {\sum_j’ \sum_{w\in V} f(w, d, j’)}$
      • cover over all topics, determine probability of document coverting certain topic
    • $p^{(n+1)}(w|\theta_j) = \frac{\sum_{d\in C} f(w, d, j)} {\sum_{w’\in V} \sum_{d\in C} f(w’, d, j)}$
      • cover over all vocalublary and documents, determine probability of word occurring under certain topic

Latent Dirichlet Allocation (LDA)

• extension of LDA
  • MAP
    • pseudo counts of w from prior $\theta’$ – as if more documents are added…
    • $p^{(n+1)}(w|\theta_j) = \frac{\sum_{d\in C} f(w, d, j) + \mu p(w|\theta_j’)} {\sum_{w’\in V} \sum_{d\in C} f(w’, d, j) + \mu}$
      • $\mu = 0$: prior is removed
      • $\mu = +\infty$: word probabilities are enforced
    • also may set certain $\pi$ to zero – not let certain topic to be generated
• deficiency of PLSA
  • not a generative model
    • cannot compute probability of a new document
      • $\pi$ is tied with training data / documents, not future
  • complex: many parameters to compute
    • many local maxima
    • prone to over-fitting
      • the model is too flexible to fit the training data
      • not able to generalise
• LDA
  • topic coverage and topic word distributions can be inferred using Bayesian inference
    • inference is still a problem: many parameters?
• PLSA -> LDA
  • $p(\vec{\pi}_d) = Dirichlet(\vec{\alpha}), \vec{\alpha} = (\alpha_1, …, \alpha_k)$
    • k topics
  • $p(\vec{\theta}_i) = Dirichlet(\vec{\beta}), \vec{\beta} = (\beta_1, …, \beta_M)$
    • M words

---

Week 3

Text Clustering: Motivation

• perspective must be defined
  • by what do one think elements are similar

Generative Probablitic Models

• one topic is a cluster
• mixture model for document clustering
  • stay with one distribution once the decision is made
  • word distribution is to be used for generating all the words in one document
• difference between topic model and clustering model:
  • topic model:
    • $p(d) = \prod_{i=1}^L [p(\theta_1)p(x_i|\theta_1) + p(\theta_2)p(x_i|\theta_2)]$
    • each word are generated in a mixture of multiple topic distributions
  • mixture model for clustering:
    • $p(d) = p(\theta_1)\prod_{i=1}^L p(x_i|\theta_1) + p(\theta_2) \prod_{i=1}^L p(x_i|\theta_2)]$
    • stay with the distribution and generate all words
• generalised form of mixture model for document clustering
  • $p(d|\Lambda) = \sum_{i=1}^k [p(\theta_i) \prod_{w\in V} p(w|\theta_i)^{c(w, d)}]$
    • unigram model
  • maximise likelihood estimate
    • $\Lambda^* = argmax_\Lambda p(d|\Lambda)$
• cluster allocation
  • $p(\theta_i)$ does not depend on d
  • likelihood + prior (Bayesian):
    • considers documents’ size
    • prefer large cluster
• example
  • normalisation to avoid underflow
    • both denominator and nominator, to divide by $\prod p(w_i|\bar{\theta})$
    • if not, $p(\theta) \prod p(w_i|\theta)$ is very small, and may not be manageable
    • or, use $\log$
    • anyway, try to preserve precision

Similarity-based Approaches

• explicitly define a similarity function to measure similarity
  • in contrast, generative model uses an implicitly defined function, e.g. likelihood function
• find an optimial partitioning of data:
  • maximise intra-group similarity
  • minimise inter-group similarity
• methods
  • hierarchical clustering, e.g. HAC
  • “flat” clustering, e.g. k-means
    • k-means is very similar to EM algorithm
      • ~ e-step: assign vector to a cluster whose centroid is the closest
        • difference: here: just assign it, exactly!
        • EM algorithm: attach a probability saying a vector belongs to some cluster
      • ~ m-step: recompute centroids
        • difference: here: exact point
        • probablitic allocation

Clustering Evaluation

• must define perspective
• closeness between clustering results and humab-generated result

Text Categorisation

• related to
  • topic mining and analysis
  • predicting / analysing the observer / author
  • prediction

Text Categorisation Methods

• (manual categorisation) works well when:
  • categories are well defined
  • categories are easily distinguished on surface features in text
  • domain knowledge is available to suggest many effective rules
• problems
  • labor intensive – doesnt scale up well
  • rules may be inconsistent (e.g. different categorisation based on different rules) – not robust
  • solvable by using machine learning

Text Categorisation: Generative Probabilistic Models

• naiive Bayes Classifier
  • if $\theta_i$ represents category i acurately
    • how? learn from the data?
    • in clustering, $\theta_i$ are adjusted to maximise likelihood function
    • (maybe, clustering first can be used as unsupervised learning to generate clustering / categorisation labels)
    • (and then, based on the result $\theta_i$, further categorisation can be conducted)
  • same as clustering
  • $category(d) = argmax_i p(\theta_i|d) = argmax_i \prod_{w\in V}p(w|\theta_i)^{c(w, d)}p(\theta_i)$
  • to avoid underflow problems, rewrite using $\log$
    • $category(d) = argmax_i \log{p(\theta_i) + \sum_{w\in V}}c(w, d) \log{p(w|\theta_i)}$
  • naiive: assume each words are generated independently
• smoothing in Naiive Bayes
  • why
    • addressing data sparseness (occurrence of zero probability)
    • incorporate prior knowledge (human direction)
    • achieve discriminative weighting
  • how (similar as before)
    • $p(\theta_i)=\frac{N_i + \delta} {\sum_{j=1}^k N_j + k\delta}$
    • $p(w|\theta_i) = \frac {\sum_{j=1}^{N_i} c(w, d_{ij} + \mu p(w|\theta_B))} {\sum_{w’\in V’} \sum_{j=1}^{N_i} c(w’, d_{ij}) | \mu}$
      • the added background words will be less important as before, because they are now considered in all categories
• anatomy of Naiive Bayes Classifier
  • logistic regression?
  • $score(d) = \beta_0 + \sum f_i \beta_i$
  • $f_i = c(w, d)$

Text Categorisation: Discriminative Classifiers

• logistic regression
  • $\log \frac{p(\theta_1)|d} {p(\theta_2|d)} = \log \frac{p(Y=1|X)} {1-p(Y=1|X)} = \beta_0 + \sum_{i=1}^M x_i \beta_i$
  • rewrite: \(p(Y=1\|X) = \frac {e^{\beta_0+\sum_{i=1}^M x_i \beta_i}}{e^{\beta_0+\sum_{i=1}^M x_i \beta_i} + 1}\)
  • maximum likelihood estimate: $\hat{\vec{\beta}} = argmax_{\vec{\beta} p(T|\vec{\beta})}$
• k-nearest neighbours (KNN)
  • assume $p(\theta_i|d)$ is locally smooth / same for all d’s in a region
    • how to determine the region? i.e. similarity
• support vector machine (SVM)
  • linear separator to maximise the margin
  • support vectors: the data points that determines the margins
    • closest data points to the separator
• summary:
  • multiple methods available
  • may produce similar results, but with different possible mistakes
  • so one can compare / combine them

Text Categorisation: Evaluation

• classification accuracy
  • problems:
    • some decision errors are more serious
    • test set is skewed
• per-document evaluation
  • precision and recall
• per-category evaluation
  • precision and recall, in a different perspective
  • combine precision and recall – F-measure
  • (macro) averaging over all categories
    • compute precision, recall and F-measure for each category / document
    • aggregate all precision, recall and F-measure
    • relatively more informative than micro-averaging
  • (micro) averaging
    • compute precision, recall and F-measure once for all documents

---

Week 4

Opinion Mining and Sentiment Analysis: Motivation

• opinion $\approx$ a subjective statement describing what a persion believes or thinks about something

Sentiment Classification

• suppose we know opinion holder & target & context & content
  • output: polarity analysis, emotion analysis (beyond polarity)
• commonly used text features
  • character n-grams
  • word n-grams
    • unigram is effective, but not for sentiment analysis
    • long n-grams are discriminative, but may cause overfitting
  • POS tag n-grams
  • word classes
  • frequent patterns
  • parse tree-based
  • pattern discovery algorithms are useful for feature construction
• feature construction for text categorisation
  • major goal: optimising the tradeoff between:
    • exhaustivity: frequent features -> high coverage
    • specificity: infrequent features -> discriminative

Ordinal Logistic Regression

• motivation: rating prediction
  • output: discrete rating $r \in {1, 2, …, k}$
  • add order to a classifier
• logistic regression for multi-level rating
  • $Y_j$ is used to judge if rating is above $j$ or not
  • the formular: \(p(r > j\|X) = \frac {e^{\alpha_j + \sum_{i=1}^M x_i \beta_{ji}}}{e^{\alpha_j + \sum_{i=1}^M x_i \beta_{ji}} + 1}\)
• problems:
  • many parameters! $(k-1) * (M + 1)$
  • these k-1 classifications are not independent – maybe we can take the advantage of this
    • dependent because pos/neg features tend to have similar effect to the final ratings
• solution: ordinal logistic regression
  • $\forall{i} = 1…M, \forall{j=3…k, \beta_{ji} = \beta_{(j-1)i}}$
  • share training data
  • now the number: $M + k-1$

Latent Aspect Rating Analysis

• motivation
  • how to infer aspect ratings
  • how to infer aspect weights
  • aspect: e.g. services, value, location, etc.
• two-staged solution
  • I: aspect segmentation
    • (augmented terms in documents?)
  • II: latent rating regression
    • sentiment weights to determine aspect ratings
      • note: sentiment weights may be different for different aspects
    • aspect weights to determine overall ratings
  • in hope of finding the latent information from the observed
• latent rating regression
  • overall rating: weighted average of aspect ratings
    • $r_d \sim N(\sum_{i=1}^k \alpha_i{d} r_i(d), \delta^2)$
    • here $\vec{\alpha}(d) \sim N(\vec{\mu}, \Sigma)$
    • and $r_i(d) = \sum {w\in V} c_i(w, d)\beta{i, w}$
  • ML estimation
  • (maybe I need to read the paper…)
• a unified generative model for LARA
  • (READ THE PAPER, AGAIN!!)
  • (basically the lecture is about the paper and its results)

Text-Based Prediction

• active learning (under machine learning)
  • how to collect data that are mostly helpful to machine learning problems
• how to generate effective predictors from text?
  • topic mining, sentiment mining, etc.

Contextual Text Mining: Motivation

• context information:
  • direct context / meta-data: time, location, etc.
  • indirect context: e.g. social networkd of the author, etc.
• usage: partioning of text

Contextual Probabilistic Latent Semantic Analysis

N/A

Mining Topics with Social Network as Context

• network supervised topic modeling
  • $\hat\Lambda = argmax_\Lambda f(p(textdata | \Lambda), r(\Lambda, network)$
  • some prior on the $\Lambda$, i.e. the parameters
    • any generative model
    • any network
    • any regulariser (the $r()$)
    • any way of combination (the $f()$)
• NetPLSA
  • prior: neighbours have similar topic distribution
    • quantify the difference of the topic coverages between every two nodes
    • and multiply this difference with the link weight between them
    • incorporate this into the objective function

Mining Causal Topics with Time Series Supervision

• iterative causal topic modeling
• measuring causality
  • Granger Casuality Test